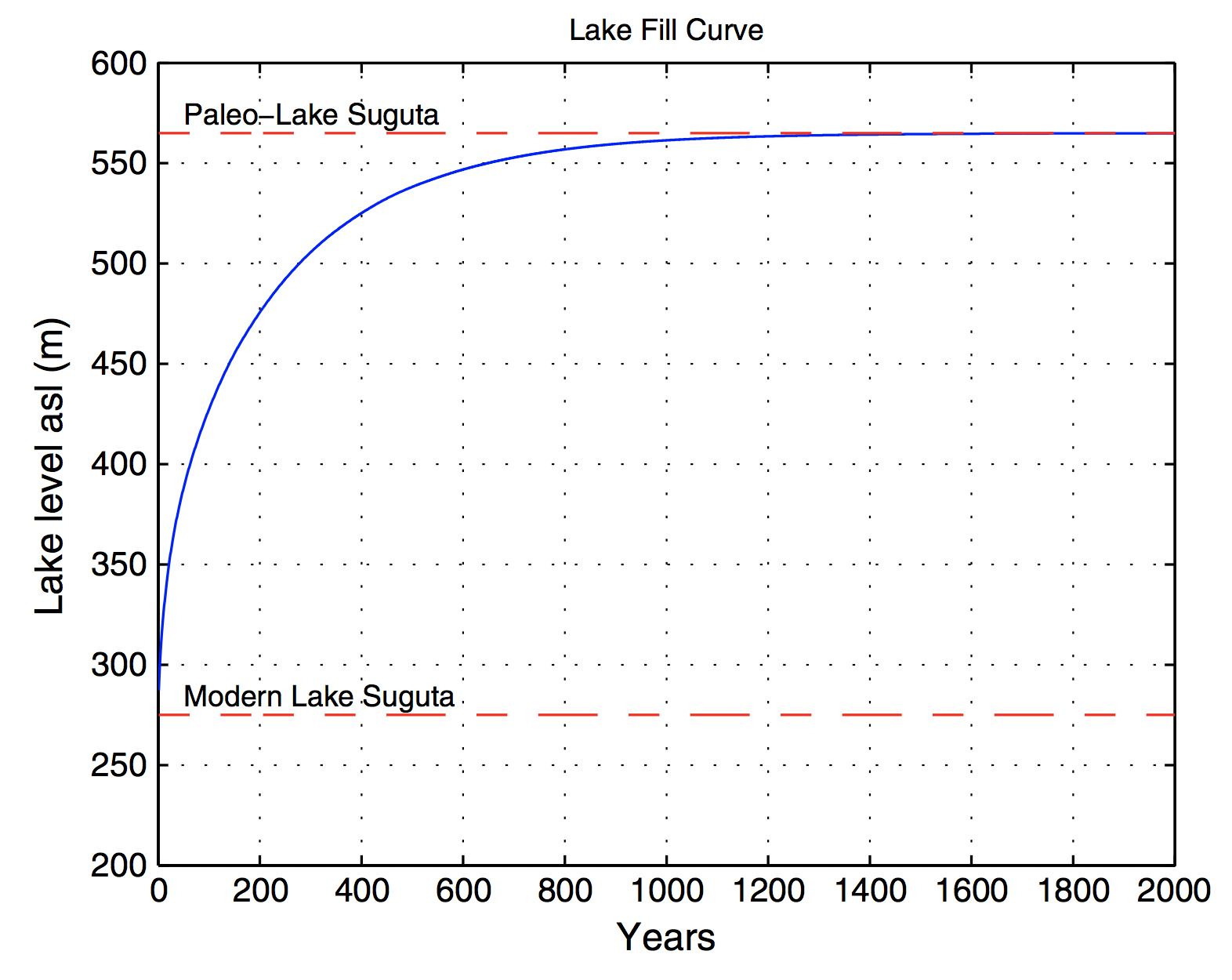
In a number of publications, we used a simple energy-based lake balance model to estimate precipitation and evaporation during highstands of paleolakes in Argentina and Kenya. The highstands were reconstructed from radiocarbon-dated paleoshorelines of landslide-dammed lakes and closed-basin rift lakes. Here we publish the MATLAB code to estimate the evaporation over land surface and water surface, which is the core of the lake-balance model used in our research.
Lake-balance models compute an equilibrium lake level for closed-basin lakes using the balance between basin-averaged precipitation and evaporation. Whereas the value of precipitation P is in principle easy to measure, evaporation E is extremely difficult to estimate. In most cases, E is calculated using empirical equations incorporating the environmental setting and climatic parameters such as temperature, relative humidity, windspeed and cloud coverage. Two different modelling approaches are commonly used for estimating evaporation with respect to atmospheric conditions, the energy-budget and bulk-transfer methods. The energy budget method evaluates the incoming and outgoing radiation at the earth’s surface. The bulk transfer method parameterizes evaporation in terms of wind speed and surface characteristics.
Working on landslide-dammed lakes in Argentina with Manfred Strecker, the idea to model the climate conditions about 30,000 years ago in the Cafayate basin in NW Argentina came from physicist and colleague Kirk Haselton. He suggest to use the Mathematica code of Lenters and Cook (1999) as a starting point for our model. Bodo Bookhagen, coadvised by Kirk Haselton and myself as a diploma student, translated the Mathematica code to MATLAB and started to model the environmental conditions when numerous large landeslides occurred in the NW Argentine Andes. I revised the model several times, before it was used by other diploma and doctoral students, such as Andreas Bergner, Miriam Dühnforth, Annett Junginger and Sven Borchardt.
The latest version is available for download and uses example parameters of a basin in East Africa. Please cite Bookhagen et al. (2001) and Lenters and Cook (1999) as the reference if you wish to use the model and the code for your own work. The paper contains a detailed description of the theoretical background and the equations used by the model. No representations are made about the suitability of this code for any purpose. It is provided as is without express or implied warranty.
Erratum
We regret that there are multiple errors in equations in the papers of Bookhagen et al. (2001), Bergner et al. (2003) and Borchardt and Trauth (2012) describing the lake-balance model. Equation (3) in Bookhagen et al. (2001) contains a superfluos variable t. In Equations (5) in both Bookhagen et al. (2001) and Bergner et al. (2003) Ts must be replaced by Ta as corrected written in Equation (5d) the cited reference by Blodgett et al. (1997) and correctly written in the MATLAB code available for download.
Interestingly, Equation (5d) in Blodgett et al. (1997) also has a mistake, as it uses the shortwave cloud parameter b instead of the longwave cloud parameter b’ to calculate the downward longwave radiation Rld , which is correct in the papers by Bookhagen et al. (2001) and Bergner et al. (2003). It should also be noted that the errors at least in Blodgett et al. (1997) as well as in Borchardt et al. (2012) the errors occurred during the typesetting process.
References
Bergner, A.G.N., Trauth, M.H., Bookhagen, B. (2003) Paleoprecipitation estimates for the Lake Naivasha basin (Kenya) during the last 175 k.y. using a lake-balance model. Global and Planetary Change, 36/1-2, 117-135.
Blodgett, T.A., Lenters, J.D., Isacks, B.L., 1997. Constraints on the origin of paleolake expansions in the Central Andes. Earth Interactions. Available online at http://EarthInteractions.org).
Bookhagen, B., Haselton, K.R., Trauth, M.H. (2001) Hydrological modelling of a Pleistocene landslide-dammed lake in the Santa Maria Basin, NW Argentina. Palaeogeography Palaeoclimatology Palaeoecology, 169, 113-127.
Borchardt, S., Trauth, M.H. (2012) Remotely-sensed evapotranspiration estimates for an improved hydrological modeling of the early Holocene mega-lake Suguta, northern Kenya Rift. Palaeogeography, Palaeoclimatology, Palaeoecology, 361-362, 14-20.
Borchardt, S., Trauth, M.H. (2020) Erratum to “Remotely-sensed evapotranspiration estimates for an improved hydrological modeling of the early Holocene mega-lake Suguta, northern Kenya Rift”. Palaeogeography, Palaeoclimatology, Palaeoecology, 109540.
Dühnforth, M., Bergner, A.G.N., Trauth, M.H. (2006) The hydrological budget of the Nakuru-Elmenteita basin, Central Kenya Rift, during the Early Holocene wet period. Journal of Paleolimnology, 36, 281-294.
Fischer, Markus L, Monika Markowska, Felix Bachofer, Verena Foerster, Asfawossen Asrat, Christoph Zielhofer, Martin H Trauth, Annett Junginger (2020) Determining the pace and magnitude of lake level changes in southern Ethiopia over the last 20,000 years using Lake Balance Modelling and SEBAL. Frontiers in Earth Science, 8, 197–XXX.
Junginger, A., Trauth, M.H. (2013) Hydrological constraints of paleo-Lake Suguta in the Northern Kenya Rift during the African Humid Period (15 – 5 ka BP). Global and Planetary Change, 111, 174–188.
