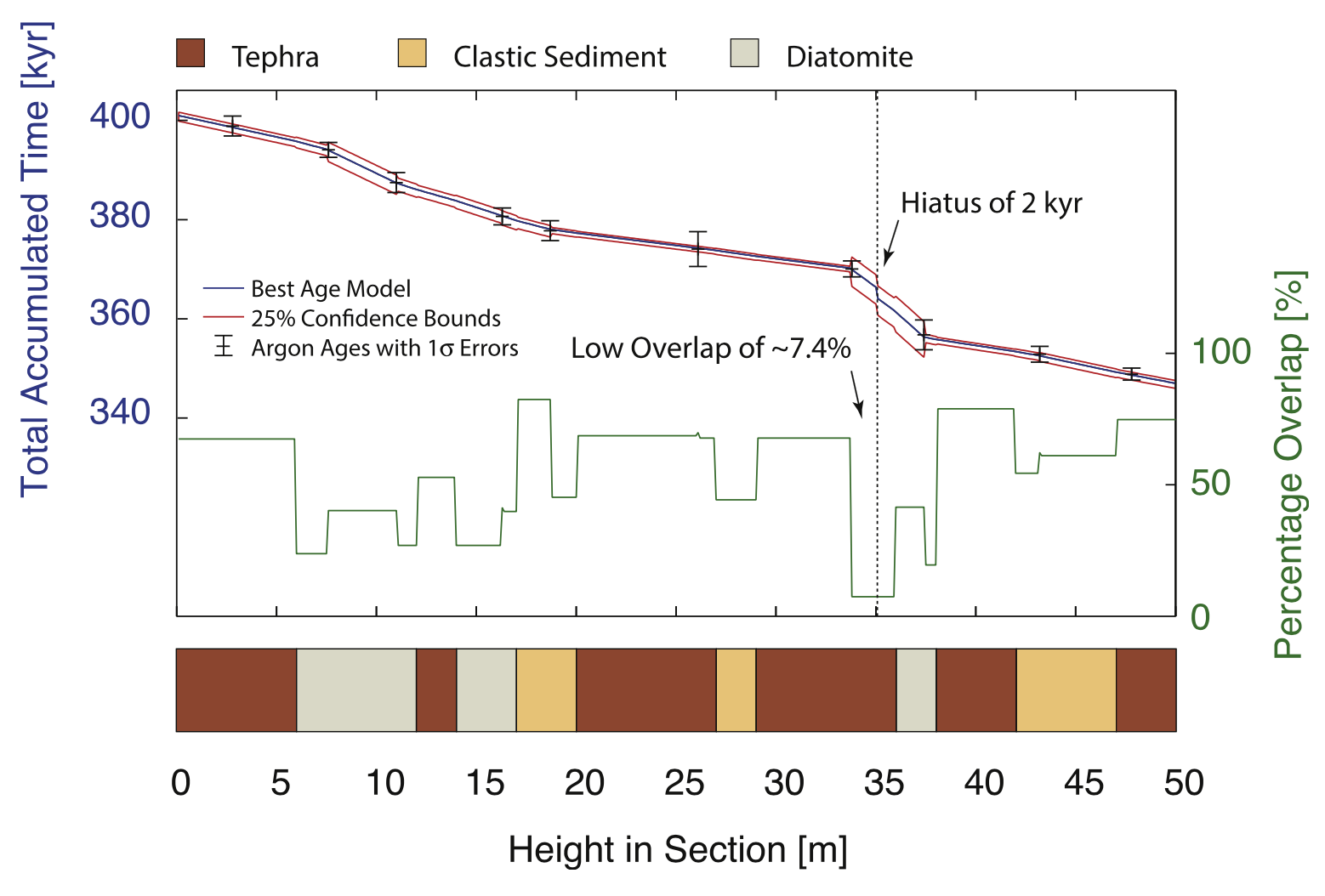
In an article published in Quaternary Geochronology (Trauth, 2014), I introduced a new method for modeling complex stratigraphic sequences. I would like to explain at this point what the result of the modeling is, and what it is not.
The age models of fluvio-lacustrine sedimentary sequences are often subject of discussions in paleoclimate research. The techniques employed to build an age model are very diverse, ranging from visual or intuitive estimation of the age-depth relationship over linear or spline interpolations between age control points to sophisticated Bayesian techniques also taking into account the most likely deposition times of the type of sediment within the sequence.
All these methods, however, fail in detecting abrupt variations in sedimentation rates, including the possibility of episodes of no deposition (hiatus), which is the strength of the method presented in this work. The new technique simply compares the deposition time of equally thick sediment slices from the differences of subsequent radiometric age dates and the unit deposition times of the various sediment types. The percentage overlap of the distributions of these two sources of information, together with the evidence from the sedimentary record, helps to build an age model of complex sequences including abrupt variations in the rate of deposition including one or many hiatuses.
It seems to be important to point out that the y-axis displays is the total accumulated time, which is the cumulative unit deposition time of the deposits, displayed together with the ±25% confidence bounds, which is different from the result of other age modeling techniques predicting ages with their confidence bounds in a given sediment depth. The unit deposition time (in kyr/m), as said in Section 2 of the paper, is the inverse of the sedimentation rate (in m/kyr), and therefore represents the time which elapses during deposition of a sediment slice of a given thickness (e.g., one meter).
As described in the paper, the method is used to detect abrupt changes in the rate of sedimentation, including times of no deposition (hiatus), and not so much to calculate ages and their uncertainties, which is a prerequisite for the correlation of the sediment record with other proxy records.
Download
Download the classic script, the live script and sample data.
Reference
Trauth, M.H. (2014) A new probabilistic technique to build an age model for complex stratigraphic sequences. Quaternary Geochronology, 22, 65-71.
